Acoustic quantities, part 1: What are decibels?

Sound is, simply put, weak but rapid fluctuations in air pressure: The air becomes a tiny bit denser, a tiny bit thinner, denser, thinner, and so forth. These fluctuations start at sound sources, for example loudspeakers, and spread out like waves. At the sound wave’s peak, the air is at its densest, while at the wave’s trough, the air is at its thinnest.

When these sound waves hit our ears, our auditory system translates them into something that we can perceive consciously — and thus, we hear that the sound is there. Still, it is difficult to describe, compare, and process these subjective experiences. For example, would you and I agree that this sound is stronger than that sound? And if so, how much stronger is it?

To make sound into something that we can measure, describe, compare, and handle, many different acoustic quantities have been introduced. We use these to make sound into something that we can discuss in a more concrete and objective manner. These quantities affect us all, not least because noise regulations use them to describe how much sound e.g. airports, roads, and concerts are allowed to make. In this article series, we will therefore go through the most important acoustic quantities. In this first part, we begin by discussing what decibels are. This is a fundamental quantity used everywhere where sound is described quantitatively.

How do we perceive loudness?

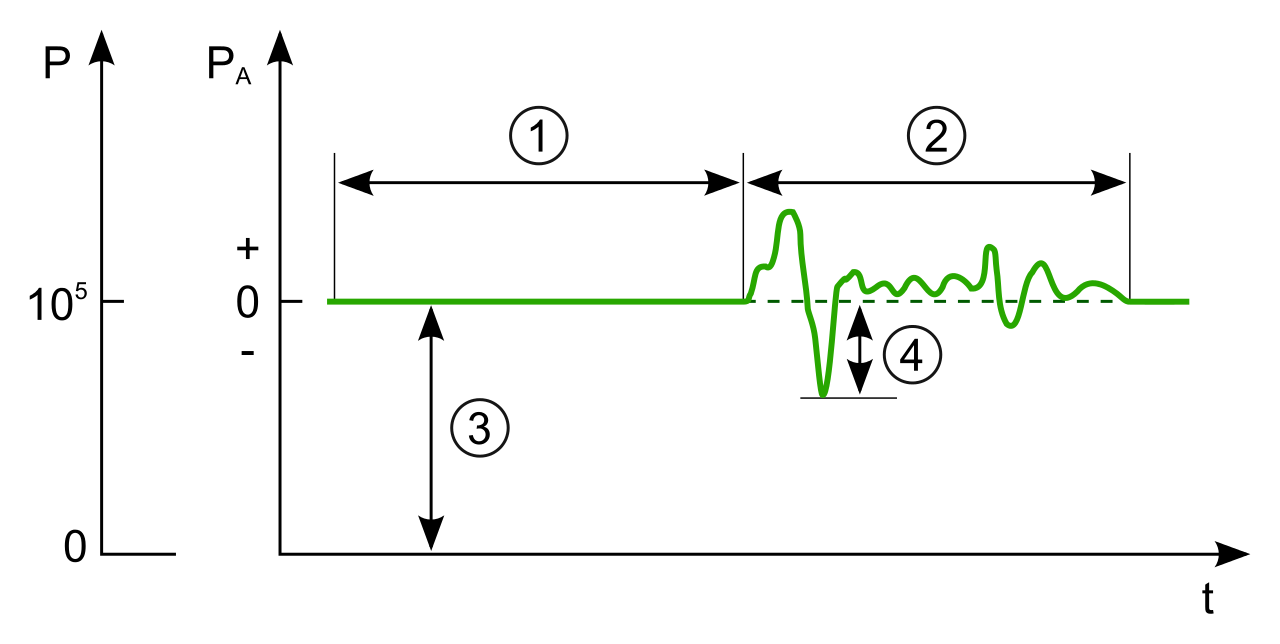
Basically, we measure sound pressure as the deviation from the approximately constant atmospheric pressure, as you can see in the figure above. (As sound pressure is thus also a kind of pressure, we measure it in the pressure unit, Pascal.) As sound waves become stronger, that is, as the pressure difference between wave peak (denser air, positive sound pressure) and wave trough (thinner air, negative sound pressure) becomes larger, we do of course also perceive that the sound becomes louder. But the manner in which we perceive it is not quite obvious. Let us have a closer look.

Let’s say that we take a sound and double its sound pressure. We perceive this as a noticeable increase in loudness. Then we take the original sound and triple its sound pressure. If we listen to these three sounds in order, most people will perceive the increase from double to triple sound pressure as weaker than the increase from original to double sound pressure. This is despite the fact that the increase, as measured in Pascals, is the same in both cases!

Instead, let’s say that we take the doubled sound pressure and double it again, so that we get the quadruple sound pressure of the original. If we compare these three sounds, we hear that we perceive increase from double to quadruple sound pressure as roughly as strong as the increase from the original to the double sound pressure. In other words, if we increase the sound by some factor (for example 2, as in this example where we double the sound pressure), most people will perceive the increase as roughly equally strong, no matter how strong the sound was originally!

You can try this out yourself:

Sound pressure	Sound
Original
Double
Triple
Quadruple

Sound pressure level and decibels

Due to the way our hearing works, it makes sense to use a logarithmic unit to describe loudness. (We will soon see why!) Sound pressure level is therefore defined as

\( L_p = 20 \times \log \left( \frac{p_\text{rms}}{p_\text{ref}} \right) \, . \)

Here, \(L_p\) is the sound pressure level in decibels (usually abbreviated to dB), \(p_\text{rms}\) is a representative sound pressure for the sound of interest, and \(p_\text{ref}\) is a reference pressure of 0.00002 Pascal (that is, 20 micro-Pascal.) When we specify loudness in decibels, it just means that we are expressing the physical sound pressure in this logarithmic form.

Why do we use decibels, though?

So, why do we actually use a logarithmic form here? From the above discussion, we know that if we for example double the sound pressure from 0.5 Pascal to 1 Pascal, and subsequently double that to 2 Pascal, we perceive both increases as roughly equally strong. But what is the sound pressure level in decibels here? If we put these numbers into the above formula, we find that the three sound pressure levels are 88 dB, 94 dB, and 100 dB. In other words, the sound pressure level increases with 6 dB every time we double the sound pressure! (Similarly, we can find that a tenfold increase in sound pressure increases the sound pressure level by 20 dB.)

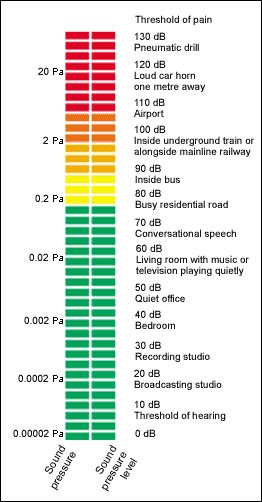
This is one reason to use decibels: If you add a certain number of decibels to a sound pressure level, you perceive the increase as roughly the same, regardless of what the original sound pressure level was. Another reason to use decibels is that human hearing spans a huge range of sound pressures. The weakest sound young people with ‘normal hearing’ can hear is about 0.00002 Pascal. The sound from a pneumatic drill — where you have to use hearing protection in order to avoid hearing damage — can be about 60 Pascal. Instead, it’s easier to say that these sounds are at 0 dB and at 130 dB.

If you are curious about the kind of levels that different common sources of sound create, the figure to the right gives an idea. You can also find nice tables and infographics on other websites. Note, however, that different sources may disagree a bit on the values for a noise source. These values vary, and are not possible to pin down exactly. For example, the loudness of conversation varies between cultures, and the loudness of road vehicles depends on vehicle type, vehicle speed, and the road surface.

(By the way, we don’t just use decibels for sound pressure. The decibel is actually a general unit of measure expressing a ratio of physical properties through a logarithmic formula as above. When you use decibels for other quantities in e.g. acoustics, electronics, and signal processing, you swap the sound pressure \(p_\text{rms}\) and reference pressure \(p_\text{ref}\) with another measurement quantity and another reference quantity.)

Representative sound pressure: RMS

As we just saw, we use a representative sound pressure \(p_\text{rms}\) to calculate the sound pressure level in decibels. From the above figure, the sound pressure varies quickly with time while the representative sound pressure \(p_\text{rms}\) is a single number. So, how do we calculate this number?

This representative sound pressure has another name as well: Root-mean-square pressure, usually abbreviated to RMS pressure. This name basically tells you how to calculate it: If we represent the pressure at time \(t\) as \(p(t)\), we first take the square of the pressure, \(p^2(t)\). Then, we take the average over this over an appropriate time period \(T\), and finally we take the square root of this. More concretely, we can express this mathematically as

\(p_\text{rms} = \sqrt{\frac{1}{T} \int_{t_0}^{t_0+T} p^2(t) \, \mathrm{d}t } \, , \)

where we choose to average from the time \(t_0\) to the time \(t_0+T\).

However, calculating a representative sound pressure in this way only makes sense for steady sounds, such as dense traffic or ventilation noise, where \(p_\text{rms}\) is quite independent of the time interval we choose for our averaging. For short, sharp sounds such as a clap or an explosion, however, \(p_\text{rms}\) would decrease with the length of the time interval, since a longer time interval means a higher proportion of silence. Later in this article series, we’ll come back to how we can find good representative sound pressure levels for such sounds as well.

Multiple sounds at the same time

Finally, we’ll look at how the sound pressure level increases when we have multiple simultaneous sounds. If we have two simultaneous sounds, e.g. two cars idling side-by-side, it’s tempting, but wrong to suppose that the sound pressure level becomes

\(20\times\log\left(\frac{p_\text{rms,1}+p_\text{rms,2}}{p_\text{rms}}\right)\,,\)

where \(p_\mathrm{rms,1}\) and \(p_\mathrm{rms,2}\) are the RMS sound pressures from car 1 and 2, respectively.

This is wrong because the sound waves from the two cars are not exactly the same. In the sound wave from the first car, the wave peaks and wave troughs won’t come at the same time as those in the sound wave from the second car. Therefore, we do not get a pure constructive interference. Rather, the two sound waves interfere partly constructively and partly destructively, so that the total RMS sound pressure becomes \(p_\mathrm{rms}=\sqrt{p_\mathrm{rms,1}^2+p_\mathrm{rms,2}^2}\). This is more than the RMS sound pressure from a single car, but less than the sum of both cars’ RMS sound pressures. (More generally, the RMS sound pressure from n different sources is \(p_\mathrm{rms}=\sqrt{\sum_{i=1}^{n}p_{\mathrm{rms},i}^2}\).)

Thus, the total sound pressure level from these two cars becomes

\(L_p=20\times\log\left(\frac{\sqrt{p_\mathrm{rms,1}^2+p_\mathrm{rms,2}^2}}{p_\mathrm{ref}}\right) \\ \phantom{L_p} =10\times\log\left(\frac{p_\mathrm{rms,1}^2+p_\mathrm{rms,2}^2}{p_\mathrm{ref}^2}\right)\,.\)

(Here we have two equivalent formulas for the sound pressure level. The first follows from what we have seen earlier, while the second is a bit more convenient to enter on your calculator. The two formulas are equal because \(20 \times \log (x) = 10 \times \log (x^2)\).)

If the two cars are equally loud (that is, if \(p_\mathrm{rms,1}=p_\mathrm{rms,2}\)), we can calculate that they together make 3 dB more sound than one car on its own. This also holds for traffic. For example, if the traffic density of a stretch of road is doubled from 2000 cars per hour to 4000 cars per hour, the total sound pressure level increases by 3 dB. This is a noticeable increase, but far from as strong as you might imagine.

Next time

At this point we have just started to examine acoustic quantities. The quantities that are used to regulate noise in various countries are more advanced, and require more explanation. Next time, we will look at frequency weighting. This lets us take into account that human ears don’t hear every sound equally well, even if the sounds’ RMS sound pressure are equal.

This post is a translation of a Norwegian-language blog post that I originally wrote for acousticsresearchcentre.no. I would like to thank Tron Vedul Tronstad for proofreading and fact-checking the Norwegian original.

Read the whole series on acoustic quantities

• Part 1: What are decibels?
• Part 2: Frequency weighting
• Part 3: Time variation
• Part 4: Quantities in noise regulations